QUADRATIC EQUATION
— — — — — — — — — —
Explanation:
How can we factor 5x^2 + 26x - 24 = 0 using the completing the square method?
Let's solve your equation step-by-step.
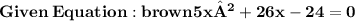
First, add 24 to both sides.
Since the coefficient of 5x² is 5, divide both sides by 5.
The coefficient of 26/5x is 26/5. So, let b=26/5.
Then we need to add (b/2)²=169/25 to both sides to complete the square.
Add 169/25 to both sides.
Factor the left side.
Take square root.
Then, add (-13)/5 to both sides.
_______________❖_______________