Question

James Perkins wants to have a million dollars at retirement, which is 15 years away. He already has $200,000 in an IRA earning 8 percent annually. How much does he need to save each year, beginning at the end of this year, to reach his target

Answer 1

Given :

James needs $ 1,000,000 after 15 years.

His IRA deposit is $ 200,000 and is earning at the rate of 8% per annum.

Maturity value of $200,000 after 15 years =
`2000000 *( 1.08)^(15)`

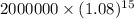
= $ 634,434.

Balance fund needed after 15 years = 1,000,000 - 634,434

= $ 365,566

Therefore, the future value of the annuity is :

`FV=A[((1+k)^n-1)/(k)]`

Here, FV = future annuity value = 365,566

A = periodical investment

k = interest rate = 8%

n = period = 15 years

∴
`365566 = A([(1.08)^(15)-1])/(0.08)`

A = 13,464

Thus, James needs to save $ 13,464 each year end to reach his target.