Answer:

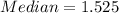
7 is an outlier
Explanation:
Given
See comment for dataset
Solving (a): The mean
The mean is calculated as:
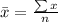
So, we have:
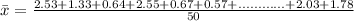


Solving (b): The median
First, we sort the data:
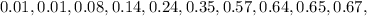
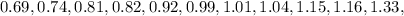
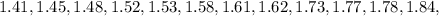
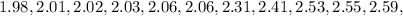
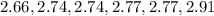
The median position is:
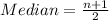
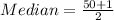
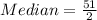
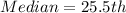
This means that the median is the average of the 25th and the 26th item.
So:
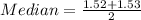
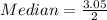
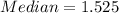
Solving (c): Is 7 an outlier
Yes; 7 is an outlier.
Because the range of the dataset (0.01 to 2.92) is far from 7.