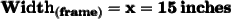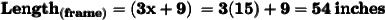Question

A frame around a rectangular family portrait has a perimeter of 138 inches. The length is nine more than three times the width. Find the length and width of the frame.

Answer 1

Given :

• Perimeter of the frame is 138 inches.
• The length is nine more than three times the width

⠀

To Find :

• The Length and width of the frame .

⠀

Solution :

We know that,

`\qquad{ \bold{ \pmb{2(Length + Breadth ) = Perimeter_((rectangle))}}}`

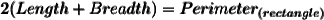
Let's assume the width of the rectangle as x inches. Then the length will become (3x + 9).

⠀

Now, Substituting the given values in the formula :

`\qquad \dashrightarrow{ \sf{2(3x + 9 + x )= 138}}`

`\qquad \dashrightarrow{ \sf{2(4x + 9 )= 138}}`

`\qquad \dashrightarrow{ \sf{8x + 18= 138}}`

`\qquad \dashrightarrow{ \sf{8x = 138 - 18}}`

`\qquad \dashrightarrow{ \sf{8x = 120}}`

`\qquad \dashrightarrow{ \sf{x = (120)/(8) }}`

`\qquad \dashrightarrow{ \bf \: x = 15}`

⠀

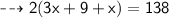
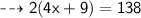
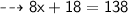
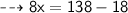
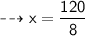
Therefore,

`\qquad { \pmb{ \bf{ Width _((frame)) = x = 15 \: inches}}}\:`

`\qquad { \pmb{ \bf{ Length _((frame)) = (3x + 9) \: = 3(15) + 9 = 54 \: inches}}}\:`