Answer:
Santos should run approximately 36.145 meters along the shore
Explanation:
The given parameters are;
The distance along the shore of the child = 50 meters
The distance from the shore of the child = 60 meters
The rate at which Santos can run = 4 m/s
The rate he can swim = 0.9 m/s
Let 'x' represent the distance he runs along the shore
We have;
The time he spends running on the shore, t₁ = x/4
The time he spends swimming, t₂ = (√(60² + (50 - x)²)/0.9
The total time, T = t₁ + t₂ = x/4 + (√(60² + (50 - x)²)/0.9
To find the maximum, we have;
dT/dx = 0 = d(x/4 + (√(60² + (50 - x)²)/0.9)/dx = 1/4 - (50 - x)/(0.9·(√(60² + (50 - x)²) = 0
1/4 - (50 - x)/(0.9·(√(60² + (50 - x)²) = 0
Simplifying using a graphing calculator gives;
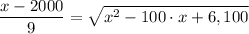
1519·x² - 151900·x + 3505900 = 0
x = (151900 ± √((-151900)² - 4×1519×3505900))/(2 × 1519)
x ≈ 63.86 m or x ≈ 36.145 m
We note that the distance from a point x = 63.83 meters and 36.145 meters from where Santos spots the girl to the location of the girl are the same
Therefore, Santos should run approximately 36.145 meters along the shore before jumping into to the water in order to save the child