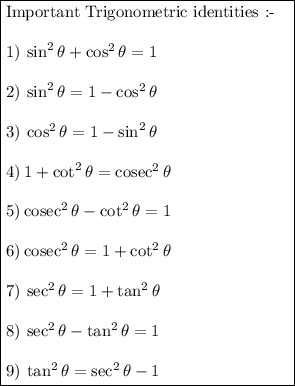Question

if sec theta + tan theta equals to X then prove that sin theta equals to x square minus x whole divided by X square + 1​

Answer 1

Question:

If sec theta + tan theta equals to x then prove that:-

`\longrightarrow \: sin \theta = \frac{ {x}^(2) - { \bold{1}} }{ {x}^(2) + 1 }`

Solution:

Given that:

`\longrightarrow \: sec \: \theta + tan \: \theta =x \: \: ..(i)`

We have to prove:

`\longrightarrow \: sin \: \theta = \frac{ {x}^(2) - 1 }{ {x}^(2) + 1}`

We know that:

`\longrightarrow \: { \sec}^(2) \theta \: - \: { \tan}^(2) \theta = 1`

`\longrightarrow ( \sec \: \theta \: + \: \tan \: \theta)( \sec \: \theta - \tan \: \theta )`

`\longrightarrow x( \sec \: \theta - \tan \: \theta) \: = 1`

`\longrightarrow \: \sec \theta - \tan \: \theta = (1)/(x) \ ..(ii)`

Adding equation (i) and (ii), we get:

`\longrightarrow \: 2\sec \theta = x + (1)/(x)`

`\longrightarrow \: 2 \sec \: \theta = \frac{ {x}^(2) + 1}{x}`

`\longrightarrow \: \sec \: \theta = \frac{ {x}^(2) + 1}{2x}`

`\longrightarrow \: \cos \: \theta = \frac{2x}{ {x}^(2) + 1 }`

Now, we know that:

`\longrightarrow \: { \sin}^(2) \theta + { \cos }^(2) \: \theta = 1`

Therefore,

`\longrightarrow \: \sin \theta \: = \sqrt{1 - { \cos }^(2) } \: \theta`

`\longrightarrow \: \sin \: \theta = {\sqrt{1 - ( \frac{2x}{ {x}^(2) + 1} } )}^(2)`

`\longrightarrow \: \sin \: \theta = \sqrt{ \frac{ {({x}^(2) + 1)}^(2) - {(2x)}^(2) }{( {x}^(2) + 1)} }`

`\longrightarrow \: \sin \: \theta = \sqrt{ \frac{ {x}^(4) \: + 2 {x}^(2) + 1 - \: 4 {x}^(2) }{( {x}^(2) { + 1)}^(2) } }`

`\longrightarrow \: \sin \: \theta = \sqrt{ \frac{ {x}^(4) - {2x}^(2) + 1 }{( {x}^(2) { + 1)}^(2) } }`

`\longrightarrow \: \sin \: \theta = \sqrt{ \frac{( {x}^(2) { - 1)}^(2) }{ {(x}^(2) + {1)}^(2) } }`

`\longrightarrow \: \sin \: \theta = \frac{ {x}^(2) - 1 }{ {x}^(2) + 1}`

Hence Proved..!!

`\:`

Learn More:

1. Relationship between sides and T-Ratios.

• sin θ = Height/Hypotenuse
• cos θ = Base/Hypotenuse
• tan θ = Height/Base
• cot θ = Base/Height
• sec θ = Hypotenuse/Base
• cosec θ = Hypotenuse/Height

2. Square formulae.

• sin²θ + cos²θ = 1
• cosec²θ - cot²θ = 1
• sec²θ - tan²θ = 1

3. Reciprocal Relationship.

• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ
• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• tan θ = 1/cot θ

4. Cofunction identities.

• sin(90° - θ) = cos θ
• cos(90° - θ) = sin θ
• cosec(90° - θ) = sec θ
• sec(90° - θ) = cosec θ
• tan(90° - θ) = cot θ
• cot(90° - θ) = tan θ

5. Even odd identities.

• sin -θ = -sin θ
• cos -θ = cos θ
• tan -θ = -tan θ

Answer 2

Correct Question :-

If sec
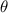`\theta` + tan
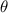`\theta`= x , then prove that ,

`\implies\sf sin\theta =(x^2-1)/(x^2+1)`

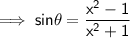
Proof :-

Here we are given that ,

`\longrightarrow \sec\theta + tan\theta = x`

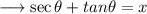
Firstly write everything in terms of sine and cosine .

`\longrightarrow (1)/(\cos\theta)+(\sin\theta)/(\cos\theta)=x`

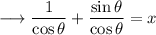
Add ,

`\longrightarrow (1+\sin\theta)/(\cos\theta)=x`

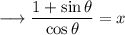
On squaring both sides , we have ;

`\longrightarrow ((\sin\theta+1)^2)/((\cos\theta)^2)=x^2`

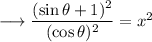
Simplify using identity sin²x + cos²x = 1 ,

`\longrightarrow ((1+\sin\theta)^2)/(1-\sin^2\theta)=x^2`

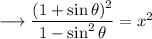
Simplify using identity (a+b)(a-b)=a²-b² ,

`\longrightarrow ((1+\sin\theta)^2)/((1+\sin\theta)(1-\sin\theta))=x^2`

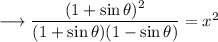
Simplify,

`\longrightarrow (1+\sin\theta)/(1-\sin\theta)=x^2`

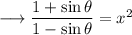
On using Componendo and Dividendo , we have ;

`\longrightarrow (1+\sin\theta+1-\sin\theta)/(1+\sin\theta-1+\sin\theta)=(x^2+1)/(x^2-1)`

`\longrightarrow (2)/(2\sin\theta)=(x^2+1)/(x^2-1)`

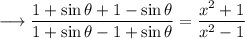
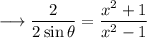
Simplify,

`\longrightarrow (1)/(\sin\theta)=(x^2+1)/(x^2-1)\\`

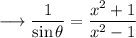
Divide both the sides by 1 ,

`\longrightarrow \underline{\underline{\sin\theta =(x^2-1)/(x^2+1)}}`

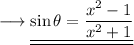
Hence proved .

And we are done !

`\rule{200}4`

More to Know :-

1) Trigonometric table :-

`\small{ \begin{tabular}c \cline{1-6} \theta & \sf 0^(\circ) & \sf 30^(\circ) & \sf 45^(\circ) & \sf 60^(\circ) & \sf 90^(\circ) \\ \cline{1-6} $ \sin $ & 0 & $(1)/(2 )$ & $(1)/( √(2) )$ & $( √(3))/(2)$ & 1 \\ \cline{1-6} $ \cos $ & 1 & $ ( √( 3 ))/(2) } $ & $ (1)/( √(2) ) $ & $ ( 1 )/( 2 ) $ & 0 \\ \cline{1-6} $ \tan $ & 0 & $ (1)/( √(3) ) $ & 1 & $ √(3) $ & $ \infty $ \\ \cline{1-6} \cot & $ \infty $ &$ √(3) $ & 1 & $ (1)/( √(3) ) $ &0 \\ \cline{1 - 6} \sec & 1 & $ (2)/( √(3)) $ & $ √(2) $ & 2 & $ \infty $ \\ \cline{1-6} \csc & $ \infty $ & 2 & $ √(2 ) $ & $ ( 2 )/( √( 3 ) ) $ & 1 \\ \cline{1 - 6}\end{tabular}}`

`\rule{200}4`

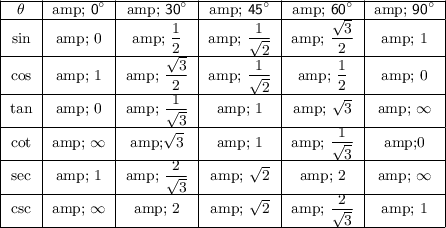
2) Important identities :-

`\boxed{\begin{minipage}{6cm} Important Trigonometric identities :- \\ \\ $\: \: 1)\:\sin^2\theta+\cos^2\theta=1 \\ \\ 2)\:\sin^2\theta= 1-\cos^2\theta \\ \\ 3)\:\cos^2\theta=1-\sin^2\theta \\ \\ 4)\:1+\cot^2\theta=\text{cosec}^2 \, \theta \\ \\5)\: \text{cosec}^2 \, \theta-\cot^2\theta =1 \\ \\ 6)\:\text{cosec}^2 \, \theta= 1+\cot^2\theta \\\ \\ 7)\:\sec^2\theta=1+\tan^2\theta \\ \\ 8)\:\sec^2\theta-\tan^2\theta=1 \\ \\ 9)\:\tan^2\theta=\sec^2\theta-1$\end{minipage}}`

`\rule{200}4`