Question

Find the value(s) of c guaranteed by the Mean Value Theorem for Integrals for the function over the given interval.

f(x) = x^7, [0, 7]

Answer 1

GIVEN: The given function is f(x)=
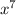`x^7` on the interval [0,7]

To FIND: Here we need to find the value of c by the help of Mean value theorem.

SOLUTION: The mean value theorem is,

`f'(c)=(f(b)-f(a))/(b-a)`

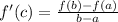
where, f(x) is defined on a closed interval [0,7] and continuous on the closed [0,7] and derivable on (0,7) and a<c<b,

So,
`f'(x)=7x^6`

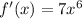
By the mean value theorem we have,

`7c^6=(7^7-0)/(7-0) \\7c^6=7^6\\c^6=7^5\\c=\sqrt[6]{7^5} \\c=5.077`

Therefore, the required value of c is 5.077