Answer: The mininum percentage of recent graduates is 88.9%
Explanation:
We are given:
Mean value = $24,800
Standard deviation = $1100
Minimum value of salary = %21,500
Maximum value of salary = %28,100
The equation for Chebyshev's Theorem is given by:
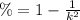 .....(1)
.....(1)
To calculate the value of 'k', we first subtract the mean value from the maximum value.
⇒ [28,100 - 24,800] = 3300
Secondly, dividing the above-calculated value by the standard deviation, we get:
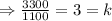
Putting value of 'k' in equation 1, we get:

Hence, the mininum percentage of recent graduates is 88.9%