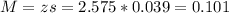Question

In a randomly selected sample of 100 students at a University, 81 of them had access to a computer at home.

a) Calculate a 99% confidence interval for the proportion of all students who had use of a computer at home and give it in interval notation.
b) Give the value of the point estimate described in this scenario.
c) Give the value of the standard error for the point estimate.
d) Give the value of the margin of error if you were to calculate a 99% confidence interval.

Answer 1

a) The 99% confidence interval for the proportion of all students who had use of a computer at home and give it in interval notation is (0.709, 0.911).

b) 0.81

c) 0.039.

d) 0.101

Explanation:

Question a:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

In a randomly selected sample of 100 students at a University, 81 of them had access to a computer at home.

This means that
`n = 100, \pi = (81)/(100) = 0.81`

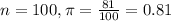
99% confidence level

So
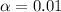`\alpha = 0.01`, z is the value of Z that has a p-value of
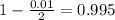`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

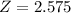The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.81 - 2.575\sqrt{(0.81*0.19)/(100)} = 0.709`

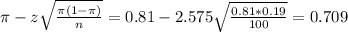
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.81 + 2.575\sqrt{(0.81*0.19)/(100)} = 0.911`

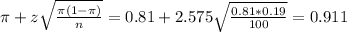
The 99% confidence interval for the proportion of all students who had use of a computer at home and give it in interval notation is (0.709, 0.911).

b) Give the value of the point estimate described in this scenario.

Sample proportion of
`\pi = 0.81`

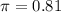
c) Give the value of the standard error for the point estimate.

This is:

`s = \sqrt{(\pi(1-\pi))/(n)} = \sqrt{(0.81*0.19)/(100)} = 0.039`

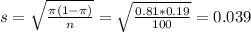
The standard error is of 0.039.

d) Give the value of the margin of error if you were to calculate a 99% confidence interval.

This is:

`M = zs = 2.575*0.039 = 0.101`