Question

State University uses thousands of fluorescent light bulbs each year. The brand of bulb it currently uses has a mean life of 600 hours. A competitor claims that its bulbs, which cost the same as the brand the university currently uses, have a mean life of more than 600 hours. The university has decided to purchase the new brand if, when tested, the evidence supports the manufacturer's claim at the .05 significance level. Suppose 100 bulbs were tested and found to have a mean of 625 hours with a standard deviation of 100. Conduct the test at the .05 level of significance. What is the test statsitic?

Answer 1

The test statistic is t = 2.5.

The p-value of the test is of 0.007 < 0.05, which means that the evidence supports the manufacturer's claim at the .05 significance level.

Explanation:

Mean life of 600 hours. Test if it is more.

At the null hypothesis, we test if the mean is of 600 hours, that is:

`H_0: \mu = 600`

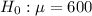
At the alternative hypothesis, we test if the mean is of more than 600 hours, that is:

`H_1: \mu > 600`

The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

600 is tested at the null hypothesis:

This means that
`\mu = 600`

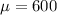
Suppose 100 bulbs were tested and found to have a mean of 625 hours with a standard deviation of 100.

This means that
`n = 100, X = 625, s = 100`.

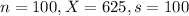Value of the test-statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (625 - 600)/((100)/(√(100)))`

`t = 2.5`

The test statistic is t = 2.5.

P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean above 625 hours, which is a right-tailed test, with t = 2.5 and 100 - 1 = 99 degrees of freedom.

Using a t-distribution calculator, this p-value is of 0.007.

The p-value of the test is of 0.007 < 0.05, which means that the evidence supports the manufacturer's claim at the .05 significance level.