Answer:
d. No because n·(1 -
 ) = 8.96 is less than 10
) = 8.96 is less than 10
Explanation:
Question options;
a. Yes because the sample sizes of both groups are greater than 5
b. Yes, because in both cases n·
 > 10
> 10
c. Yes, because we know that the population is evenly distributed
d. No, because the n·(1 -
 ) is less than 10
) is less than 10
Explanation;
The given data are;
The number of men in the sample of men, n₁ = 41
The proportion of men who dislike anchovies,
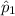 = 0.67
= 0.67
The number of women in the sample of women, n₂ = 56
The proportion of men who dislike anchovies,
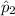 = 0.84
= 0.84
The assumptions for an analysis of the difference between means using a T-test are;
1) The data should be from a random sample of the population
2) The variables should be approximately normal (n·
 ≥ 10, and n·(1 -
≥ 10, and n·(1 -
 ) ≥ 10)
) ≥ 10)
3) The scale of the data is a continuous ordinance scale
4) The sample size should be large
5) The sample standard deviations should be approximately equal
From the requirement for normality, we have;
For the sample of men, n₁·
 ₁ = 41 × 0.67 = 24.47 > 10
₁ = 41 × 0.67 = 24.47 > 10
n₁·(1 -
 ₁) = 41 × (1 - 0.67) = 13.53 > 10
₁) = 41 × (1 - 0.67) = 13.53 > 10
For the sample of women, n₂·
 ₂ = 56 × 0.84 = 47.04 > 10
₂ = 56 × 0.84 = 47.04 > 10
n₂·(1 -
 ₂) = 56 × (1 - 0.84) = 8.96 < 10
₂) = 56 × (1 - 0.84) = 8.96 < 10
Therefore, the for n₂·(1 -
 ₂), the sample does not meet the requirement for normality
₂), the sample does not meet the requirement for normality
The correct option is d. No because n₂·(1 -
 ₂) = 8.96 is less than 10
₂) = 8.96 is less than 10