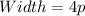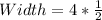Answer:
 --- equation
--- equation
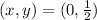 --- focus
--- focus
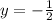 --- directrix
--- directrix
 ---- focal width
---- focal width
Explanation:
Given
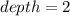
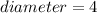
Required
The equation of parabola
The depth represents the y-axis. So:
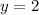
The diameter represents how the parabola is evenly distributed across the x-axis.
We have:
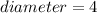
-2 to 2 is 4 units.
So:
![x = [-2,2]](https://img.qammunity.org/2022/formulas/mathematics/high-school/6rdqove8wlx7gb1qcupnjjjmn9uug5kine.png)
So, the coordinates of the parabola is:
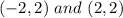
The equation of the parabola is calculated using:
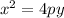
Substitute (-2,2) for (x,y)
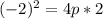
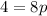
Divide by 8
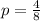
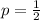
So, the equation is:
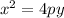
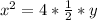

The defining features
(a) Focus
The focus is located at:

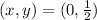
(b) Directrix (y)
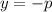
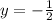
(c) Focal width