Answer:
○ B.
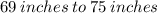
Step-by-step explanation:
The Empirical Rule states that sixty-eight percent of the population will be within one standard deviation of the mean in height. Therefore, you perfourm the operations below:
![\displaystyle \boxed{75} = 3[1] + 72 \\ \boxed{69} = -3[1] + 72](https://img.qammunity.org/2023/formulas/mathematics/college/m7qsf3145cjlojwb0uxtfsjexysjfeincx.png)
I am joyous to assist you at any time.