Answer: The ratio of thicknesses of glycerine (refractive index 1.473) to crystalline quartz (refractive index 1.544) is 0.954.
Step-by-step explanation:
Given: Refractive index of glycerine = 1.473
Refractive index of crystalline quartz = 1.544
Formula used is as follows.
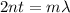
For crystalline quartz:

For glycerine:
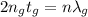
Here, m = n and

So, the ratio of both these values can be written as follows.
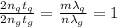
So,
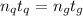

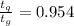
Thus, we can conclude that the ratio of thicknesses of glycerine (refractive index 1.473) to crystalline quartz (refractive index 1.544) is 0.954.