Answer: 1344 committees can be formed of four people not from one class
Step-by-step explanation:
We are given:
Members in freshmen = 6
Members in sophomores = 6
Members in juniors = 6
To form a committee of four people not from one class, numerous combinations can occur. They are:
- When in a committee, at least one of them are from each class
When 2 from freshmen, 1 from sophomores, and 1 from junior. The possibility becomes
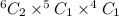
When 1 from freshmen, 2 from sophomores, and 1 from junior. The possibility becomes
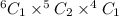
When 1 from freshmen, 1 from sophomores, and 2 from junior. The possibility becomes

Total combinations:
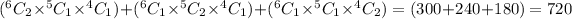
- If two members come from same class
When 2 from freshmen, 2 from sophomores, and 0 from junior. The possibility becomes
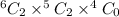
When 0 from freshmen, 2 from sophomores, and 2 from junior. The possibility becomes
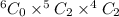
When 2 from freshmen, 0 from sophomores, and 2 from junior. The possibility becomes
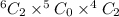
Total combinations:
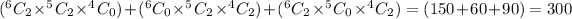
- If three members come from same class
When 3 from freshmen, 1 from sophomores, and 0 from junior. The possibility becomes
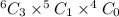
When 3 from freshmen, 0 from sophomores, and 1 from junior. The possibility becomes
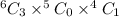
When 0 from freshmen, 3 from sophomores, and 1 from junior. The possibility becomes

When 1 from freshmen, 3 from sophomores, and 0 from junior. The possibility becomes
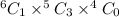
When 0 from freshmen, 1 from sophomores, and 3 from junior. The possibility becomes
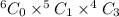
When 1 from freshmen, 0 from sophomores, and 3 from junior. The possibility becomes
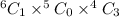
Total combinations:
![[(^6C_3* ^5C_1* ^4C_0)+(^6C_3* ^5C_0* ^4C_1)+(^6C_0* ^5C_3* ^4C_1)+(^6C_1* ^5C_3* ^4C_0)+(^6C_0* ^5C_1* ^4C_3)+(^6C_1* ^5C_0* ^4C_3)]=(100+80+40+60+20+24)=324](https://img.qammunity.org/2022/formulas/mathematics/college/1b0pbh8em0ue3kxgadlfemn2qrqlqe09i6.png)
Total number of committees that can be formed = [720 + 300 + 324] = 1344
Hence, 1344 committees can be formed of four people not from one class