Answer:
a) The difference is of 3.222 lbs.
b) 1.64 standard deviations.
c) Z = 1.64
d) Not significant, as the z-score of 1.64 is between -2 and 2.
Explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The mean of all of the weights is x=2.088 lb, and the standard deviation of the weights is s=1.968 lb.
This means that
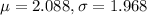
a. What is the difference between the weight of 5.31 lb and the mean of the weights?
This is

The difference is of 3.222 lbs.
b. How many standard deviations is that [the difference found in part (a)]?
This is the z-score. So


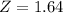
1.64 standard deviations.
c. Convert the weight of 5.31 lb to a z score.
Z = 1.64, as found above.
d. If we consider weights that convert to z scores between −2 and 2 to be neither significantly low nor significantly high, is the weight of 5.31 lb significant?
Not significant, as the z-score of 1.64 is between -2 and 2.