Question

Water is boiled in a pan covered with a poorly fitting lid at a specified location. Heat is supplied to the pan by a 2-kW resistance heater. The amount of water in the pan is observed to decrease by 1.1908 kg in 30 min. If it is estimated that 75 percent of electricity consumed by the heater is transferred to the water as heat, determine the local atmospheric pressure in that location. Use data from the tables.

Answer 1

Answer: The local atmospheric pressure in that location is 86.1 kPa.

Step-by-step explanation:

Using the rate of evaporation and rate of heat transfer the heat of evaporation is calculated as follows.

`h_(evap) = (Q)/(m)\\= (nW)/(m)\\= (0.75 * 2 kJ/kg)/((1.19)/(30 * 60))\\= 2268.9 kJ/kg`

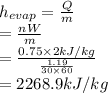
Now, using enthalpy of vaporization the local atmospheric pressure is determined from data in A-5 using interpolation:

`P = P^(*)_(1) + (P^(*)_(2) - P^(*)_(1))/(h^(*)_(2) - h^(*)_(1)) (h_(evap) - h^(*)_(1))\\= 75 kPa + ((100 - 75))/((2257.5 - 2278)) * (2268.9 - 2278) kPa\\= 86.1 kPa`

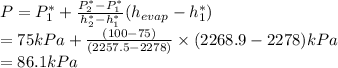
Thus, we can conclude that the local atmospheric pressure in that location is 86.1 kPa.