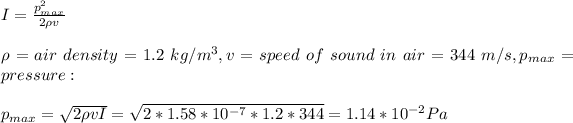Answer:
The answer is below
Step-by-step explanation:
The intensity level (B) of a sound wave is given by:
B = 10log(I/I₀);
where I₀ is the threshold intensity = 1 * 10⁻¹² W/m², I is the intensity at distance 5 m, B is the intensity level = 52 dB
Substituting gives:
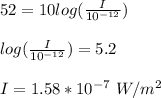
The pressure is given by: