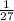Answer:
Explanation:
Since there are a total of three buckets and only one can be chosen at a time, this would mean that the probability of a ball being placed in a bucket is 1/3. Since each ball has the same probability of being placed into any bucket regardless of the where the previous ball landed, it means that each ball has the same 1/3 probability of a bucket. In order to find the probability that all three land in the same bucket, we need to multiply this probability together for each one of the balls like so...
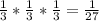
Finally, we see that the probability of all three balls landing in the same bucket is