Question

A swimmer bounces straight up from a diving board and falls feet first into a pool. She starts with a velocity of 4.00 m/s, and her takeoff point is 1.80 m above the pool. We assume the upward direction to be positive, and the downward direction to be negative.

(a) How long are her feet in the air?(b) What is her highest point above the board?(c) What is her velocity when her feet hit the water?

Answer 1

(a) t = 1.14 s

(b) h = 0.82 m

(c) vf = 7.17 m/s

Step-by-step explanation:

(b)

Considering the upward motion, we apply the third equation of motion:

`2gh = v_f^2 - v_i^2`

where,

g = - 9.8 m/s² (-ve sign for upward motion)

h = max height reached = ?

vf = final speed = 0 m/s

vi = initial speed = 4 m/s

Therefore,

`(2)(9.8\ m/s^2)h = (0\ m/s)^2-(4\ m/s)^2\\`

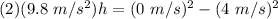
h = 0.82 m

Now, for the time in air during upward motion we use first equation of motion:

`v_f = v_i + gt_1\\0\ m/s = 4\ m/s + (-9.8\ m/s^2)t_1\\t_1 = 0.41\ s`

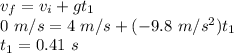
(c)

Now we will consider the downward motion and use the third equation of motion:

`2gh = v_f^2-v_i^2`

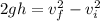
where,

h = total height = 0.82 m + 1.8 m = 2.62 m

vi = initial speed = 0 m/s

g = 9.8 m/s²

vf = final speed = ?

Therefore,

`2(9.8\ m/s^2)(2.62\ m) = v_f^2 - (0\ m/s)^2\\`

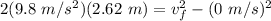
vf = 7.17 m/s

Now, for the time in air during downward motion we use the first equation of motion:

`v_f = v_i + gt_1\\7.17\ m/s = 0\ m/s + (9.8\ m/s^2)t_2\\t_2 = 0.73\ s`

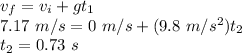
(a)

Total Time of Flight = t = t₁ + t₂

t = 0.41 s + 0.73 s

t = 1.14 s