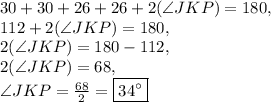Question

If P is the incenter of JKL, find m Please show the work, that would be really helpful, thank you!

Answer 1

`34^(\circ)`

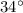
Explanation:

The incenter of a triangle can be defined as the intersection of three angle bisectors that bisect all angles of the triangle.

By definition, an angle bisector divides an angle into two equal smaller angles.

Therefore:

`\angle KJN=\angle LJN,\\\angle KLM=\angle JLM, \\\angle JKP=\angke LKP`

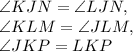
What we're given:

• 
  `\angle KJN=\angle LJN=30^(\circ)`
• 
  `\angle KLM=\angle JLM=26^(\circ)`

The sum of the interior angles of a triangle always add up to be 180 degrees. Since these six angles make up the total sum of the interior angles, we have the following equation:

`\angle KJN+\angle LJN+\angle KLM +\angle KLM +\angle JKP+ \angle LKP=180^(\circ)`

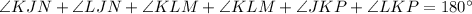
Substituting given values:

`30+30+26+26+\angle JKP+\angle LKP=180`

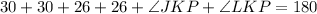
Since
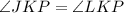`\angle JKP=\angle LKP`,

`30+30+26+26+2(\angle JKP)=180,\\112+2(\angle JKP)=180,\\2(\angle JKP)=180-112,\\2(\angle JKP)=68,\\\angle JKP=(68)/(2)=\boxed{34^(\circ)}`