Answer:
The probability of obtaining a sample mean less than or equal to $8.85 per hour=0.0082
Explanation:
We are given that
Average wage,
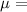 $9.00/hour
$9.00/hour
Standard deviation,
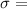 $0.50
$0.50
n=64
We have to find the probability of obtaining a sample mean less than or equal to $8.85 per hour.

Using the values
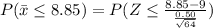
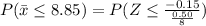
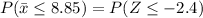
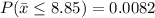
Hence, the probability of obtaining a sample mean less than or equal to $8.85 per hour=0.0082