Answer: A 10,000-Hz sound is 10 times more intense as compared to a 1000-Hz sound to be perceived as equal to 60 phons of loudness.
Step-by-step explanation:
The formula used is as follows.
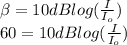
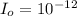 normal threshold
normal threshold
The difference is sound level is as follows.
60 - 60 = 0
Hence,
![0 = 10 dB [log ((I_(f))/(I_(o))) - log ((I_(i))/(I_(o)))]\\log ((1000)/(I_(o))) = log ((10000 x)/(I_(o)))\\log (10^(15)) = log (10^(16)x)\\15 = 16 + log x\\log x = 1\\x = 10](https://img.qammunity.org/2022/formulas/physics/college/jrya55m6w5d2z0virhk48hnmean19xe23q.png)
This means that 10,000 Hz sound is 10 times more intense.
Thus, we can conclude that a 10,000-Hz sound is 10 times more intense as compared to a 1000-Hz sound to be perceived as equal to 60 phons of loudness.