Question

There are 750 identical plastic chips numbered 1 through 750 in a box. What is the probability of reaching into the box and randomly drawing a chip number that is smaller than 627

Answer 1

The probability of randomly drawing a chip number smaller than 627 is 313/375.

Step-by-step explanation:

To find the probability of randomly drawing a chip number that is smaller than 627, we need to determine the number of chips that are smaller than 627 and divide it by the total number of chips.

The number of chips smaller than 627 is 626 (since the chips are numbered from 1 to 750).

Therefore, the probability is 626/750, which can be simplified to 313/375.

Answer 2

0.8358 = 83.58% probability of reaching into the box and randomly drawing a chip number that is smaller than 627

Step-by-step explanation:

Uniform probability distribution:

An uniform distribution has two bounds, a and b.

The probability of finding a value of at lower than x is:

`P(X < x) = (x - a)/(b - a)`

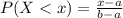
There are 750 identical plastic chips numbered 1 through 750 in a box

This means that
`a = 1, b = 750`

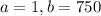
What is the probability of reaching into the box and randomly drawing a chip number that is smaller than 627?

`P(X < x) = (627 - 1)/(750 - 1) = 0.8358`

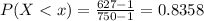
0.8358 = 83.58% probability of reaching into the box and randomly drawing a chip number that is smaller than 627