Answer: At a value of 12.3 the mean should be set so that 99.9% of all cans exceed 12 fluid ounces.
Explanation:
Let us assume that X is a normal rando variable with a mean value
 and standard deviation
and standard deviation
 .
.
Hence, random variable Z will be introduced as follows.

(a) Set the value
 and the equation will be written down as follows.
and the equation will be written down as follows.
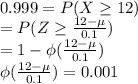
According to the tables,
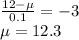
Thus, we can conclude that at a value of 12.3 the mean should be set so that 99.9% of all cans exceed 12 fluid ounces.