Question

Danielle has test scores of 92, 86, 83, 90 and 91 in her math class. What score does she need on the next test to have an overall class average of 90%?

Answer 1

98

Explanation:

An average score can be calculated by finding the sum of all scores and then dividing by the number of tests. So we can create an equation like this:

`((92+86+83+90+91+x))/(6)=90`

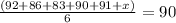
The numerator is the sum of her scores, where x represents the score of her next test (which is what we're trying to find).

The denominator is the total number of tests, which is 6 - this includes the 5 she has taken already and the next test that she hasn't taken yet.

Furthermore, we know all of this has to equal 90 because that's the average we're looking for.

Now we just solve for x.

Step 1) Multiply by 6:

`92+86+83+90+91+x=90 * 6`

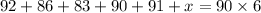
Step 2) Simplify equation:

`442+x=540`

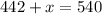
Step 3) Subtract 442:

`x=540-442=98`

Therefore, x = 98, so Danielle must achieve a score of 98 to have an overall class average of 90.