Question

In a certain​ region, about 11​% of a​ city's population switches from phone service provider APP to phone service provider BPP each​ year, and about 5% of the populaton switches from BPP to APP each year. Show the system of linear equations that models this migration pattern to calculate the new amounts of the population with each service provider. In​ 2018, there were 1.75 million customers of APP and 2.05 million customers of BPP. Find the predicted number of customers for each provider in 2022. Round to the nearest hundredth of a million when reporting the populations.

Answer 1

The predicted number of customers for APP in 2022 is of 1.37 million, and of BPP is of 2.59 million.

Explanation:

Exponential function:

An exponential function has the following format:

`y(t) = y(0)r^t`

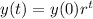
In which
`y(0)` is the initial value and r is the rate of change.

11​% of a​ city's population switches from phone service provider APP to phone service provider BPP each​ year, and about 5% of the populaton switches from BPP to APP each year.

This means that each year, the BPP amount increases by 11 - 5 = 6%, and the APP decreases by 6%. So the equations are:

BPP:

`B(t) = B(0)(1 + 0.06)^t`

`B(t) = B(0)(1.06)^t`

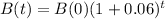
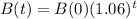
APP:

`A(t) = A(0)(1 - 0.06)^t`

`A(t) = A(0)(0.94)^t`

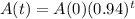
In​ 2018, there were 1.75 million customers of APP and 2.05 million customers of BPP.

This means that
`A(0) = 1.75, B(0) = 2.05`

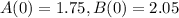
Thus

`B(t) = 2.05(1.06)^t`

`A(t) = 1.75(0.94)^t`

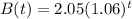
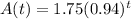
Find the predicted number of customers for each provider in 2022.

2022 - 2018 = 4, so we have to find A(4) and B(4).

`B(4) = 2.05(1.06)^4 = 2.59`

`A(4) = 1.75(0.94)^4 = 1.37`

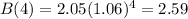
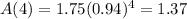
The predicted number of customers for APP in 2022 is of 1.37 million, and of BPP is of 2.59 million.