Answer: The lowest possible frequency of sound for which this is possible is 212.5 Hz.
Step-by-step explanation:
It is known that formula for path difference is as follows.
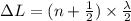 ... (1)
... (1)
where, n = 0, 1, 2, and so on
As John is standing perpendicular to the line joining the speakers. So, the value of
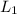 is calculated as follows.
is calculated as follows.
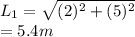
Hence, path difference is as follows.
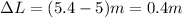
For lowest frequency, the value of n = 0.
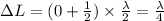
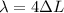
where,
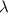 = wavelength
= wavelength
The relation between wavelength, speed and frequency is as follows.
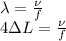
where,
 = speed
= speed
f = frequency
Substitute the values into above formula as follows.
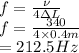
Thus, we can conclude that the lowest possible frequency of sound for which this is possible is 212.5 Hz.