Answer:
TN = 13 units
MP = 22 units
TQ = 6.93 units
PT = 13 units
Explanation:
If T is a circumcenter of the given triangle MNP,
Measure of TN = Measure of TM = Measure of TN
By applying Pythagoras theorem in ΔMRT,
MT² = TR² + MR²
MT² = (12)² + 5²
MT =
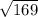
MT = 13
Measure of TN = 13 units
Since, TQ, TS and RT are the perpendicular bisectors of the sides MP, NP and MN respectively,
Measure of MP = 2(PQ)
= 2(11)
= 22 units
By applying Pythagoras theorem in ΔTQM,
MT² = TQ² + MQ²
(13)² = TQ² + (11)²
TQ =
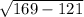
TQ =
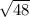
TQ = 6.93
Measure of PT = Measure of TN = 13 units