Answer:
D. 91%
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Less than 15 minutes.
Event B: Less than 10 minutes.
We are given the following probability distribution:
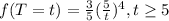
Simplifying:
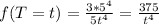
Probability of arriving in less than 15 minutes:
Integral of the distribution from 5 to 15. So

Integral of
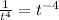 is
is
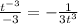
Then
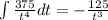
Applying the limits, by the Fundamental Theorem of Calculus:
At
 ,
,
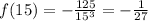
At
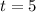 ,
,
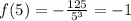
Then
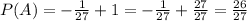
Probability of arriving in less than 15 minutes and less than 10 minutes.
The intersection of these events is less than 10 minutes, so:

We already have the integral, so just apply the limits:
At
 ,
,
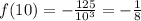
At
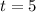 ,
,
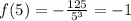
Then

If given the train arrived in less than 15 minutes, what is the probability it arrived in less than 10 minutes?
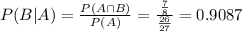
Thus 90.87%, approximately 91%, and the correct answer is given by option D.