Answer:
a) The force that the worker must apply has a magnitude of 75.317 newtons.
b) The external force does a work of 0.301 joules.
c) The friction force does a work of -0.301 joules.
d) Both normal force and gravity have done a work of 0 joules.
e) The total work done on the crate is 0 joules.
Step-by-step explanation:
a) As the crate is moving at constant velocity, we know that magnitude of the force done on the crate must be equal to the friction force. Hence, we must use the following formula:
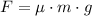 (1)
(1)
Where:
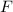 - External force, in newtons.
- External force, in newtons.
 - Coefficient of kinetic friction, no unit.
- Coefficient of kinetic friction, no unit.
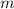 - Mass, in kilograms.
- Mass, in kilograms.
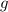 - Gravity acceleration, in meters per square second.
- Gravity acceleration, in meters per square second.
If we know that
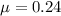 ,
,
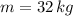 and
and
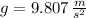 , then the external force is:
, then the external force is:
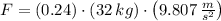
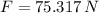
The force that the worker must apply has a magnitude of 75.317 newtons.
b) The direction of the force is parallel to the direction of motion. The work done by this force (
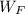 ), in joules, is determined by this formula:
), in joules, is determined by this formula:
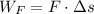 (2)
(2)
Where
 is the distance travelled by the crate, in meters.
is the distance travelled by the crate, in meters.
If we know that
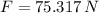 and
and
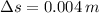 , then the work done by the force is:
, then the work done by the force is:
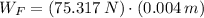
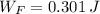
The external force does a work of 0.301 joules.
c) The direction of the friction force is antiparallel to the direction of motion. The work done by this force (
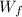 ), in joules, is determined by this formula:
), in joules, is determined by this formula:
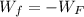 (3)
(3)
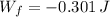
The friction force does a work of -0.301 joules.
d) The direction of the normal force is perpendicular to the direction of motion. Therefore, no work is done due to normal force.
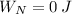
Likewise, no work is done by gravity.
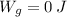
Both normal force and gravity have done a work of 0 joules.
e) The total work is the sum of the works done by the external force and the friction force:
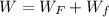
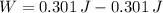
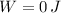
The total work done on the crate is 0 joules.