Question

Calculate the mean, the variance, and the standard deviation of the following discrete probability distribution. (Negative values should be indicated by a minus sign. Round intermediate calculations to at least 4 decimal places. Round your final answers to 2 decimal places.)

x −36 −26 −15 −4
P(X = x) 0.32 0.36 0.21 0.11
Mean
Variance
Standard deviation

Answer 1

Mean = 24.47

Variance = 108.31

Standard deviation = 10.41

Explanation:

The probability distribution table has been attached to this response.

(1) To calculate the mean (m)

(a) First multiply each of the values of x by their corresponding probability values.

This is shown in the third column of the table.

(b) The sum of the results in the third column gives the mean of the distribution. i.e

m = ∑xP(x) = 11.52 + 9.36 + 3.15 + 0.44

m = 24.47

(2) To calculate the variance (σ²).

(a) First find the square of the difference between the values of x and the mean (m) calculated in (1b) above. i.e

(x - m)²

The result is shown in the fourth column of the table.

(b) Next, multiply each of the results in the fourth column (x - m)², by their corresponding probability values P(X = x). i.e

(x - m)²(P(X = x))

The result is shown in the fifth column of the table.

(c) Now find the variance (σ²) which is the sum of the results in the fifth column. i.e

σ² = ∑(x - m)²(P(X = x)) = 42.5411 + 0.8427 + 18.8330 + 46.0923

σ² = 108.3091

σ² = 108.31 [to 2 decimal places]

(3) To calculate the standard deviation (σ)

The standard deviation is the square root of the variance of the distribution. Calculate this by finding the square root of the result in (2c) above.

σ = √σ²

σ =
`√(108.31)`

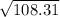
σ = 10.4072

σ = 10.41 [to 2 decimal places]