Question

A 97.0 kg ice hockey player hits a 0.150 kg puck, giving the puck a velocity of 48.0 m/s. If both are initially at rest and if the ice is frictionless, how far does the player recoil in the time it takes the puck to reach the goal 14.5 m away

Answer 1

s₁ = 0.022 m

Step-by-step explanation:

From the law of conservation of momentum:

`m_1u_1 + m_2u_2 = m_1v_1+m_2v_2`

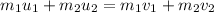
where,

m₁ = mass of hockey player = 97 kg

m₂ = mass of puck = 0.15 kg

u₁ = u₂ = initial velocities of puck and player = 0 m/s

v₁ = velocity of player after collision = ?

v₂ = velocity of puck after hitting = 48 m/s

Therefore,

`(97\ kg)(0\ m/s)+(0.15\ kg)(0\ m/s)=(97\ kg)(v_1)+(0.15\ kg)(48\ m/s)\\\\v_1 = -((0.15\ kg)(48\ m/s))/(97\ kg) \\v_1 = - 0.074 m/s`

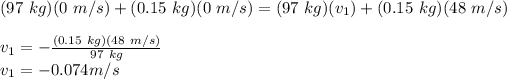
negative sign here shows the opposite direction.

Now, we calculate the time taken by puck to move 14.5 m:

`s_2 =v_2t\\\\t = (s_2)/(v_2) = (14.5\ m)/(48\ m/s) \\\\t = 0.3\ s`

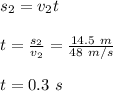
Now, the distance covered by the player in this time will be:

`s_1 = v_1t\\s_1 = (0.074\ m/s)(0.3\ s)`

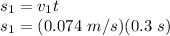
s₁ = 0.022 m