Question

5. If R(2.2) and S(5.4) i. Calculate the magnitude of RS ii. Express RS in the form (K,D), where K is the magnitude and Q the bearing. ​

Answer 1

We have:

R = (2, 2)

S = (5, 4)

RS is the segment that connects R with S.

So RS is just the distance between R and S.

Remember that the distance between two points (a, b) and (c, d) is given by:

`distance = √((a - c)^2 + (b - d)^2)`

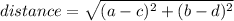
Then the distance between S and R is

`distance = √((5 - 2)^2 + (4 - 2)^2) = √(3^2 + 2^2) = √(13)`

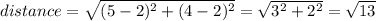
Then:

RS = √13

ii) Now we want to express RS in the form (K, Q)

where K is the magnitude (we already know that it is √13) and Q is the bearing, which is measured with respect to the horizontal axis.

To interpret the bearing, let's look at the image below:

We can use the relation:

Tan(θ) = (opposite cathetus)/(adjacent cathetus)

where the opposite cathetus is just the difference between the y-values:

Opposite cathetus = 4 - 2 = 2

And the adjacent cathetus is the difference between the x-values:

Adjacent cathetus = 5 - 2 = 3

Then we have:

Tan(θ) = 2/3

If we apply the inverse tangent equation to both sides, we get:

Atan(tan(θ)) = Atan(2/3)

θ = Atan(2/3) = 33.69°

The bearing is 33.69°

then:

RS = (√13, 33.69°)