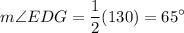Answer:
Problem 1)
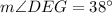
Problem 2)
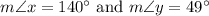
Problem 3)
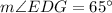
Explanation:
Problem 1: ∠DEG
From the diagram, we know that ∠DFG intercepts Arc DG.
Inscribed angles have half the measure of its intercepted arc. Therefore:
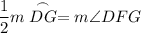
We know that m∠DFG = 38°. So:

∠DEG also intercepts Arc DG. Hence:

We know that Arc DG measures 76°. Hence:
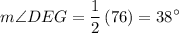
Alternate Explanation:
Since ∠DEG and ∠DFG intercept the same arc, ∠DEG ≅ DFG. So, m∠DEG = m∠DFG = 38°.
Problem 2: Circle with Centre O
(Let the bottom left corner be A, upper be B, and right be C.)
∠ACB intercepts Arc AC.
Inscribed angles have half the measure of its intercepted arc. Therefore:
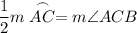
Since m∠ACB = 70°:
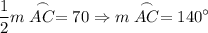
∠x is a central angle and also intercepts Arc AC.
The measure of a central angle is equal to its intercepted arc. Thus:
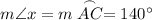
The sum of the interior angles of a polygon is given by the formula:
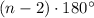
Where n is the number of sides.
Since the inscribed figure is a four-sided polygon, its interior angles must total:

Therefore:
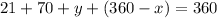
Substitute and solve for y:
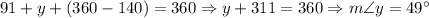
Problem 3: ∠EDG
∠EFG intercepts Arc EDG.
Inscribed angles have half the measure of its intercepted arc. Therefore:
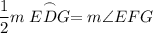
Since m∠EFG = 115°:
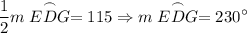
A full circle measures 360°. Hence:
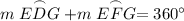
Since we know that Arc EDG measures 230°:
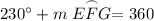
Solve for Arc EFG:
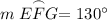
∠EDG intercepts Arc EFG.
Inscribed angles have half the measure of its intercepted arc. Therefore:
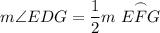
Since we know that Arc EFG measures 130°: