Answer:
Tiana will earn approximately $50,841 with her investment amount total to be $134,768.
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra II
Compounded Interest Rate Formula:
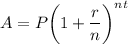
- P is principal amount
- r is rate
- n is compound rate
- t is time
Explanation:
Step 1: Define
Identify variables.
P = $83,927
r = 0.07
n = 1
t = 7
Step 2: Find Return Investment
- Substitute in variables [Compounded Interest Rate Formula]:
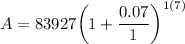
- [Order of Operations] Evaluate parenthesis:
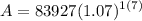
- [Order of Operations] Simplify exponents:
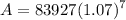
- [Order of Operations] Evaluate exponents:
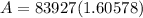
- [Order of Operations] Multiply:
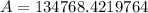
- Find difference:
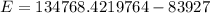
- [Order of Operations] Subtract:
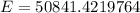
- Round:
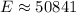
∴ After Tiana invests $83,927 with a 7% interest compounded annually in a timeframe of 7 years, she would make $50,841 with a total account value of $134,768.
---
Topic: Algebra II