Question

Given right triangle ABC= with altitude BD drawn to hypotenuse AC. If AD=3 and, AC=27, what is the length of AB?

Answer 1

Given:

In a right angle triangle ABC, altitude BD drawn to hypotenuse AC.

AD=3 and, AC=27.

To find:

The length of AB.

Solution:

Draw a figure by using the given information as shown below.

In triangle ABC and ADB,

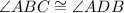`\angle ABC\cong \angle ADB` (Right angles)

`\angle BAC\cong \angle DAB` (Common angle)

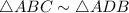`\triangle ABC\sim \triangle ADB` (AA similarity postulate)

We know that the corresponding parts of congruent triangles are proportional. So,

`(AC)/(AB)=(AB)/(AD)`

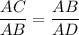
After substituting the given values, we get

`(27)/(AB)=(AB)/(3)`

`27* 3=AB* AB`

`81=AB^2`

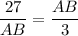
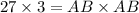
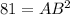
Taking square root on both sides, we get

`√(81)=AB`

`9=AB`

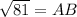
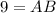
Therefore, the length of AB is 9 units.