Answer: No real number solutions
The complex number solutions are
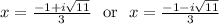
where

=======================================================
Step-by-step explanation:
The given equation 3x^2+2x+4 = 0 is in the form ax^2 + bx + c = 0
We have
Let's compute the discriminant.
d = b^2 - 4ac
d = (2)^2-4(3)(4)
d = -44
The result is negative, so there are no real number solutions.
----------------
If you wanted to find the complex valued solutions, then we apply the quadratic formula.
Plug in a = 3, b = 2, c = 4

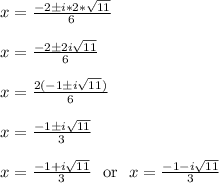
Notice in step 3 we have -44 under the square root. The negative value in the square root leads directly to the imaginary number

Though the term "imaginary" is a bit unfair and misleading because numbers like -22 are just as imaginary and made up by humans. It just depends on context in which imaginary numbers are useful (eg: with physics or engineering).