Question

HELP PLSSS I HAVE AN EXAM MONDAY AND I THINK THIS IS GONNA BE ON ITTTT

A fish is at the western bank of a river that is 64 m wide and has a current with a velocity of 0.90 m/s [S]. The fish swims directly across the river going due east. The fish can swim at a speed of 0.2 m/s.

a) How long does it take for the fish to get across the river
b) What is the resulting velocity of the fish
c) When the fish arrives on the opposite bank, how far is it from being at the point directly across from where it started?

The answers are here, please show work on how to get these
a) 3.2 x 10^2
b) 0.9 m/s (S 13 E)
c) 2.9 x 10^2

Answer 1

(a) 3.2 x 10²s

(b) 0.9 m/s (S 13 E)

(c) 2.9 x 10²m

Step-by-step explanation:

The sketch illustrating the scenario has been attached to this response.

As shown;

The fish swims due east with a velocity
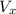`V_(x)` = 0.2m/s

The river current has a velocity
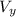`V_(y)` due South = 0.9m/s

The resultant of the velocity is V

The width of the river is x = 64m

(a) To calculate how long it took the fish to get across the river, we know that velocity is the rate of change in distance, therefore we can use the relation;

V =
`(d)/(t)` -------------(i)

Where;

V = velocity of the fish =
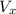`V_(x)` = 0.2m/s

d = distance from the start to the end = width of the river = x = 64m

t = time taken to move for that distance

Make t subject of the formula in equation (i);

t =
`(d)/(V)`

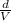
Substitute the values of d and V into the equation;

t =
`(64m)/(0.2m/s)`

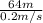
t = 320 s

t = 3.20 x 10²s

Therefore, the time taken for the fish to get across the river is 3.20 x 10²s

(b) The resulting vector of the fish is V whose magnitude is the algebraic sum of vectors
`V_(x)` and
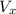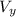`V_(y)`, and direction is given by θ. i.e

The magnitude of the resulting vector is;

|V| =
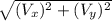
`√((V_x)^2 + (V_y)^2)`

|V| =
`√((0.2)^2 + (0.9)^2)`

|V| =
`√((0.04) + (0.81))`

|V| =
`√((0.85))`

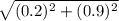
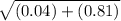
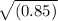
|V| = 0.92m/s

|V| ≅ 0.9m/s

The direction of the resulting vector θ and is given by;

tan θ =
`(V_y)/(V_x)`

tan θ =
`(0.9)/(0.2)`

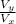
tan θ = 4.5

θ = tan⁻¹ ( 4.5)

θ = 77.47° South of East.

θ ≈ 77.5° South of East.

Subtracting θ = 77.5° from 90° gives its value East of South

i.e

90 - 77.5 = 12.5° East of South

This can also be written as S12.5°E

Approximating to the nearest whole number gives S 13 E

Therefore, the resulting velocity of the fish is 0.9m/s in the direction S13°E

(c) When the fish arrives on the opposite bank, its distance from being at the point directly across from where it started is the product of the velocity of the river current and the time taken by the fish to get across the river. This point is equivalent to k as shown in the diagram.

Therefore;

distance = velocity of river current x time taken

distance = 0.9m/s x 3.20 x 10²s

distance = 2.88 x 10²m

distance ≅ 2.9 x 10²m

Notice that the velocity of the river current is used since that's the velocity of the fish on the y-axis.