Question

1. Five men takes 3 hours and 20 minutes paint a house. How long would it take four men to paint a similar house? Give your answer in hours and minutes.

2. If 24 houses can be built by 6 builders in one year, how many builders would it take to build 52 houses in the same amount of time?

3. Two people can build four identical walls in three days. At this rate, how many of these walls could ten people build in 3.75 days?

4. Two toy makers can make eight toy soldiers in two weeks. How many toy soldiers could seven toy makers make in three weeks if they work at the same rate?

Answer 1

Explanation:

1. Let s = the speed of one painter. Then the equation for this is a variation of the d = rt where r is speed, d is the number of houses painted, and time is the time in hours. If that be the case, then our equation in terms of speed, number of houses, and time is

s = #houses/time. If there are 5 painters and it takes them 3 1/3 hours, then the equation fills in as

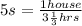`5s=(1house)/(3(1)/(3)hrs )` solve for s. We are going to simplify the right side a bit first:

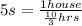`5s=(1house)/((10)/(3)hrs )` and simplifying a bit more:

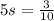`5s=(3)/(10)` and multiply both sides by 1/5 to get

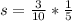`s=(3)/(10)*(1)/(5)` so

s =
`(3)/(50)`.

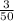If we want to find out how long it takes 4 painters to paint the same house, the equation for that will be very close to the one we started out with but with 4 painters instead of 5:

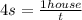`4s=(1house)/(t)` where t is our unknown for these 4 painters. Subbing in for s:

`4((3)/(50))=(1)/(t)` and

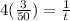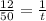`(12)/(50)=(1)/(t)` and cross multiply to get the answer:

12t = 50 and

t = 4 1/3 hrs so

t = 4 hours and 20 minutes.

2. This one is easy. It's a proportion:

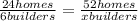`(24homes)/(6builders)=(52homes)/(xbuilders)` and cross multiply:

24x = 312 so

x = 13 builders

3. Not quite as easy, but the logic is easy to follow, so I'll explain as I go along, ok?

If it takes 2 people to build 4 walls in 3 days, then this group of 2 people can build 4/3 walls in one day. Since there are 5 groups of 2 people in 10 people total, then 5(4/3) is the number of walls per day that 5 groups of 2 can build, which is 20/3 walls per day. If they work for 3.75 days (which is 15/4 in an improper fraction), then

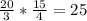`(20)/(3)*(15)/(4)=25` walls

4. Is almost exactly the same thing as 3. If a group of 2 makers make 8 toys in 2 weeks, then this group of 2 can make 4 toys in 1 week. There are 3.5 groups of 2 in 7 makers, so 3.5(4) = 14 toys in one week by 3.5 groups of 2. Multiply this by 3 weeks to get 42 toys.