Question

URGENT: If θ is a second-quadrant angle and cosθ = -2/3, then tanθ = _____.

Answer 1

In the second quadrant, both cos and tan are negative while only sin is positive.

To find tan, we will use the following property below:

`\large \boxed{ {tan}^(2) \theta = {sec}^(2) \theta - 1}`

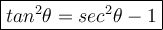
Sec is the reciprocal of cos. If cos is a/b then sec is b/a. Since cos is 2/3 then sec is 3/2

`\large{ {tan}^(2) \theta = {( - (3)/(2)) }^(2) - 1} \\ \large{ {tan}^(2) \theta = (9)/(4) - 1} \\ \large{ {tan}^(2) \theta = (9)/(4) - (4)/(4) \longrightarrow (5)/(4) } \\ \large{tan \theta = ( √(5) )/( √(4) ) } \\ \large \boxed{tan \theta = ( √(5) )/(2) }`

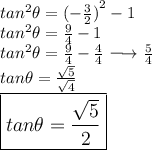
Since tan is negative in the second quadrant. Hence,

`\large{ \cancel{ tan \theta = ( √(5) )/(2) } \longrightarrow \boxed{tan \theta = - ( √(5) )/(2) }}`

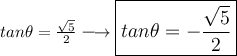
Answer

• tan = -√5/2