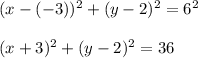Question

Determine the equation of the circle graphed below.

( please help me )

Answer 1

`Equation : \\(x+3)^2 + ( y -2)^2 = 36`

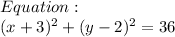
Explanation:

For standard form the circle's equation we need the centre of the circle and the radius.

Step 1: Find the centre

If the centre is not given find the end points of the diameter

and then find the mid point.

Let the end points of the diameter be : ( - 3 , 8 ) and ( -3 , -4 )

The mid-point of the diameter is :

`Mid-point = ((-3 + - 3)/(2), (-4+8)/(2)) = (-3, 2)`

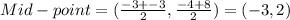
Therefore, centre of the circle = ( -3 , 2 )

Step 2 : Find radius

`Radius = (Diameter )/(2)`

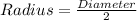
Diameter is the distance between the end points ( -3 , 8) and ( -3 , -4 )

That is ,

`Diameter = √((-3-(-3))^2 + ( -4 -8)^2)\\`

`= √((-3 + 3)^2 + (-12)^2)\\\\=√(0 + 144)\\\\=12`

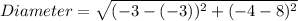
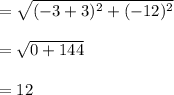
Therefore ,

`Radius = (12)/(2) = 6`

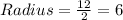
Step 3 : Equation of the circle

Standard equation of the circle with centre ( h ,k )

and radius ,r is :

`(x - h)^2+(y -k)^2 = r^2`

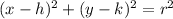
Therefore, the equation of the circle with centre ( -3, 2)

and radius = 6 is :

`(x - (-3))^2 + (y - 2)^2 = 6^2\\\\(x + 3)^2 + (y - 2)^2 = 36`