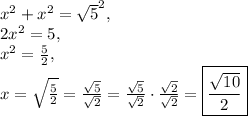Answer:
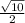
Explanation:
The diagonal forms two 45-45-90 triangles, with the diagonal being the hypotenuse of both. The Pythagorean Theorem states that
 , where
, where
 is the hypotenuse of the triangle, and
is the hypotenuse of the triangle, and
 and
and
 are the two legs of the triangle.
are the two legs of the triangle.
From the Isosceles Base Theorem, the two legs of a 45-45-90 triangle are always equal. Since we're given a diagonal of
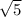 , we have:
, we have: