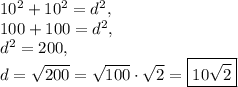Question

The figure is a square. Find the length of side x in simplest radical form with a rational denominator.

Answer 1

`10√(2)`

Explanation:

The diagonal of any square with side length
`s` is equal to
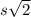`s√(2)`. Since the side length of the square is 10, the diagonal must be
`\boxed{10√(2)}`.

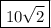To support and prove this:

The diagonal creates two 45-45-90 triangles, with the diagonal being the hypotenuse of both of these triangles. The Pythagorean Theorem states that in any triangle, the sum of the squares of both legs is equal to the square of the hypotenuse (
`a^2+b^2=c^2`).

Call the diagonal
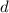`d`. In these two triangles, both legs are equal to 10 (the side lengths of the square), and the hypotenuse is the diagonal. Thus, we have:

`10^2+10^2=d^2,\\100+100=d^2,\\d^2=200,\\d=√(200)=√(100)\cdot √(2)=\boxed{10√(2)}`

Answer 2

Explanation:

The side making up the top triangle is also 10.

a^2 + b^2 = x^2 Pythagoras

Givens

a = b Property of a square

a = 10

b = 10

Solution

10^2 + 10^2 = x^2

100 + 100 = x^2

x^2 = 200

x^2 = 2 * 100

sqrt(x^2) = sqrt(2 * 100)

x = 10*sqrt(2)