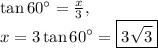Question

Find the length of side x in simplest radical form with a rational denominator.

Answer 1

`3√(3)`

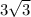
Explanation:

In all 30-60-90 triangles, the side lengths are in the ratio
`x:x√(3):2x`, where
`x` is the side opposite to the 30 degree angle and
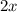`2x` is the hypotenuse of the triangle. Since the side opposite to the 30 degree angle is marked as 3, the value of
`x` must be
`\boxed{3√(3)}`.

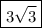Alternatively, we can use basic trig. for a right triangle to solve. In any right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side. Thus, we have:

`\tan 60^(\circ)=(x)/(3),\\x=3\tan 60^(\circ)=\boxed{3√(3)}`

Answer 2

Explanation:

The tangent of a 60 degree angle = Sin(60) / Cos(60)

Sin(60) = Square root (3) / 2

Cos(60) = 1/2

Tan(60) = √3 / 2 // 1/2 Invert the denominator and multiply

Tan(60) = √3/2 * 2/1

Tan(60) = √3

Tan(theta) = opposite / adjacent

Tan(theta) = x/3 in this case

Tan(60) = √3 = x/3

x = 3*√3