Question

I need help please someone help me

Answer 1

We know that the height equation is given by:

H(t) = -16*t^2 + 108*t + 28

in ft.

First, we want to find the maximum height of the ball.

The first thing we can see is that the leading coefficient of the quadratic equation is negative, this means that the arms of the graph will open downwards, so the vertex of the quadratic equation is the maximum.

We also know that the ball will reach its maximum height when its velocity is zero (this means that the object stops going upwards at this point).

To get the velocity equation we need to derivate the above equation, we will get:

V(t) = 2*(-16)*t + 1*108

V(t) = -32*t + 108

We need to find the value of t such that this is zero, we will get:

V(t) = 0 = -32*t + 108

32*t = 108

t = 108/32 = 3.375

So the ball reaches its maximum height after 3.375 seconds.

Then the maximum height is given by the height equation evaluated in that time, we will get:

H(3.375) = -16*(3.375)^2 + 108*3.375 + 28 = 210.25

Then the maximum height of the ball is 210.25 ft

The ball will hit the ground when:

H(t) = 0

Then we just need to solve:

0 = -16*t^2 + 108*t + 28

Using the Bhaskara's equation we can find that the two solutions for t are:

`t = (-108 \pm √((108)^2 - 4*(-16)*28) )/(2*(-16)) = (-108 \pm 116)/(-32)`

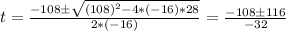
So the two solutions are:

t = (-108 + 116)/-32 = -0.25

t = (-108 - 116)/-32 = 7

Because t represents time, we should take only the positive value of time (as t = 0 is the time when the ball is thrown).

Then we can conclude that the ball hits the ground after 7 seconds.