Question

Solve each triangle. Round your answers to the nearest tenth.
show work If possible ​

Answer 1

∠ABC = 76°

BC = 20.1

CA = 28.0

Explanation:

Solving the triangle means finding all unknown angles and sides of the triangle.

(i) Two of the angles (∠BCA = 60° and ∠CAB = 44°) are given. To find the third angle (∠ABC), use one of the theorems stating that the sum of angles of a triangle is equal to 180°.

Therefore, the sum of angles of the triangle ABC is 180°. i.e

∠ABC + ∠BCA + ∠CAB = 180°

=> ∠ABC + 60° + 44° = 180°

=> ∠ABC + 104° = 180°

=> ∠ABC = 180° - 104°

=> ∠ABC = 76°

(ii) One side (BA) of the triangle is given. To get the other sides, we use the sine rule as follows;

=>
`(sin60)/(25) = (sin44)/(BC) = (sin76)/(CA)`

=>
`(sinBCA)/(BA) = (sinCAB)/(BC) = (sinABC)/(CA)`

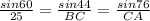
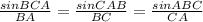
Substitute the necessary values

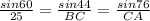`(sin60)/(25) = (sin44)/(BC) = (sin76)/(CA)` ---------------------(ii)

(a) To get side BC, use the first two terms of equation (ii)

`(sin60)/(25) = (sin44)/(BC)`

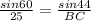
Cross multiply

BC x sin 60 = 25 x sin 44

BC x 0.8660 = 25 x 0.6947

0.8660 x BC = 17.3675

BC =
`(17.3675)/(0.8660)`

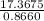
BC = 20.05

=> BC = 20.1 to the nearest tenth

(b) To get CA, use any two terms of equation (ii). Using the first and third terms, we have;

`(sin60)/(25) = (sin76)/(CA)`

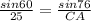
Cross multiply

CA x sin 60 = 25 x sin 76

CA x 0.8660 = 25 x 0.9703

0.8660 x CA = 24.2575

CA =
`(24.2575)/(0.8660)`

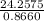
CA = 28.01

=> CA = 28.0 to the nearest tenth