Question

Use trigonometric identities to verify each expression is equal. sin(x)/1-cos(x)-cot(x)=csc(x)

Answer 1

See Below.

Explanation:

We want to verify the identity:

`\displaystyle (\sin x)/(1 - \cos x) - \cot x = \csc x`

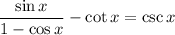
We can multiply the fraction by 1 + cos(x):

`\displaystyle (\sin x(1+\cos x))/((1 - \cos x)(1+\cos x)) - \cot x = \csc x`

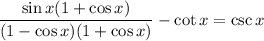
Difference of Two Squares:

`\displaystyle (\sin x(1+\cos x))/(1-\cos^2 x) - \cot x = \csc x`

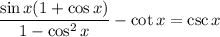
From the Pythagorean Theorem, we know that sin²(x) + cos²(x) = 1. Rearranging, we acquire that sin²(x) = 1 - cos²(x). Substitute:

`\displaystyle (\sin x(1+\cos x))/(\sin^2 x) - \cot x = \csc x`

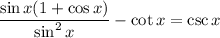
Cancel:

`\displaystyle ( 1 + \cos x)/(\sin x)-\cot x = \csc x`

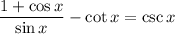
Let cot(x) = cos(x) / sin(x):

`\displaystyle ( 1 + \cos x)/(\sin x)-(\cos x)/(\sin x) = \csc x`

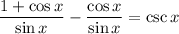
Combine Fractions:

`\displaystyle ( 1 + \cos x - \cos x)/(\sin x)= \csc x`

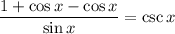
Thus:

`\displaystyle (1)/(\sin x)=\csc x = \csc x`

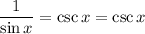
Hence proven.