Given:
The different functions in the form of set of ordered pairs.
To find:
The function which has an inverse that is also a function.
Solution:
A relation is a function if there exists unique y-value for each x-value.
We know that the inverse transformation is defined as:

So, the inverse of function is also a function if their exists unique x-value for each y-value in the function.
In option A, all x-values and y-values are unique. It means, inverse of this function is also a function. So, option A is correct.
In option B,
 and
and
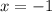 when
when
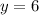 . It means, inverse of this function is not a function. So, option B is incorrect.
. It means, inverse of this function is not a function. So, option B is incorrect.
In option C,
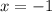 and
and
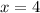 when
when
 . It means, inverse of this function is not a function. So, option C is incorrect.
. It means, inverse of this function is not a function. So, option C is incorrect.
In option D,
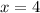 and
and
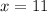 when
when
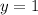 . It means, inverse of this function is not a function. So, option D is incorrect.
. It means, inverse of this function is not a function. So, option D is incorrect.
Therefore, the correct option is A.