Answer:
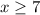
 ∈
∈
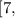 ∞
∞

Explanation:
In this problem, one is given the following function,
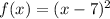
The problem asks one to find the interval for which the function is one-to-one and non-decreasing.
A one-to-one function is when every element in the range corresponds to every element in the range. Moreover, no element in the range will correspond to more than one element in the domain. In essence, every input pairs to only one output, and every output pairs to only one input. In a quadratic equation (an equation with a term to the second degree (exponent of (2)), half of the graph will form a one-to-one function. This is because when one has the full graph, for every output there are two inputs. However, with half of the graph, there is only one input for every output. Therefore, a function with a domain of all values less than the (x-coordinate) of the vertex will form a one-to-one function. The same conclusion can be drawn for any value greater than the (x-coordinate) of the vertex.
The given function is in vertex form. This means that one can find the vertex using the given information. The general format for the vertex form of a quadratic equation is as follows,
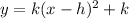
Where vertex is the following,
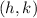
Applying this logic here, one can state that the vertex of the given equation (
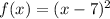 ) is as follows,
) is as follows,
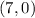
Since the coefficient of this equation is positive (no coefficient means that it is (1)) outside of it, one can conclude that the graph of the equation is increasing after the (x) value of (7). Therefore, the function is one-to-one and increasing on the interval (
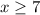 ).
).